GETTING AROUND: SHORTEST ROUTES ON NETWORKS
Dr. G.V.V. Jagannadha Rao
Department of Mathematics
Assistant Professor
Dr.gvvj.rao@kalingauniversity.ac.in
Keywords: Shortest Path, Edges, Nodes, pathways, Network.
We choose the routes to take every day to get from one point to another. You may go from your bedroom to the kitchen in your house. You could commute to college from your house outside. Imagine we have a network a grouping of things (referred to as “nodes”) and the links (referred to as “edges”) that connect them. of locations that are connected to one another through roads and paths. Each of these places is referred to as a node. The elements of a network that are interconnected. For instance, in Figure 1, each location and each junction of a street is referred to as a node, while the streets and walkways are referred to as edges.a thing that joins two nodes together.
In mathematics, individuals look at path lengths to build short paths. A shortest path can frequently be found to be beneficial. A path between two nodes that has the fewest edges a measure of how much effort it takes to go along an edge in a network—is said to be the shortest path. In real life, a cost could represent something else, like time or distance. it is the same to go down each edge (for instance, if each edge is a roadway that has the same length). A shortest path is a path from an origin node to a destination node that has the lowest overall cost among all pathways from the origin to the destination, given an origin node and a destination node.
One adds the individual costs of each of a path’s edges to determine its cost. A cost may be used to gauge time, space, or another factor. The quickest route from home to college, for instance, may be the one that requires the least amount of time out of all the alternatives in the tiny city map depicted in Figure 1. Because many pathways might have the same minimal cost, there may be more than one shortest path between any two nodes in a network. For this reason, even if it seems strange, we talk about “a” shortest path between two nodes rather than “the” shortest path between them.
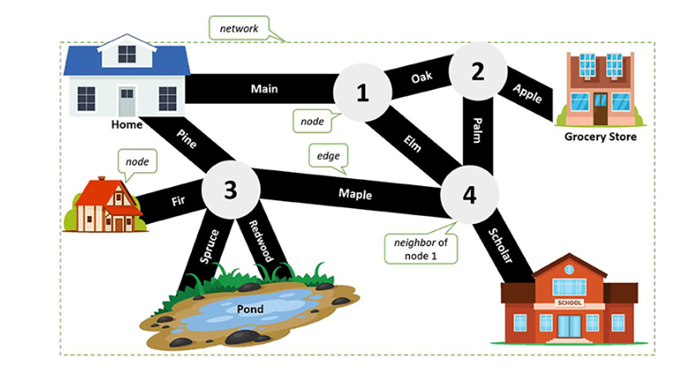
Figure 1: Location Map of small town
When you go to multiple locations in your everyday life, you presumably already consider the shortest routes. In our bedroom-to-kitchen example, if you merely wanted to go from your bedroom to your kitchen, it would not make much sense to walk from your bedroom to the laundry room, then outside to your backyard, and then back inside to your kitchen. Walking straight from your bedroom to your kitchen without pausing in the laundry room and backyard would be significantly faster. There aren’t many street crossings (also known as nodes) on a journey where the destinations are near to one another, therefore you can potentially try out the majority of the various pathways to determine the quickest route.
Finding the shortest trip is significantly more challenging if the places are farther away, like as your house, college, and a grocery store in a separate city. How does navigational software like Google Maps decide which route is the most effective for getting somewhere? Finding a path between two nodes that minimizes the total cost of the path’s edges is a solution to the mathematical issue known as the shortest path.
We will measure distance in the same manner that we would measure it between two points on the floor in your home since we are assuming everything is two-dimensional (like a sketch on a sheet of paper). Things like height and the curvature of the Earth won’t concern us.
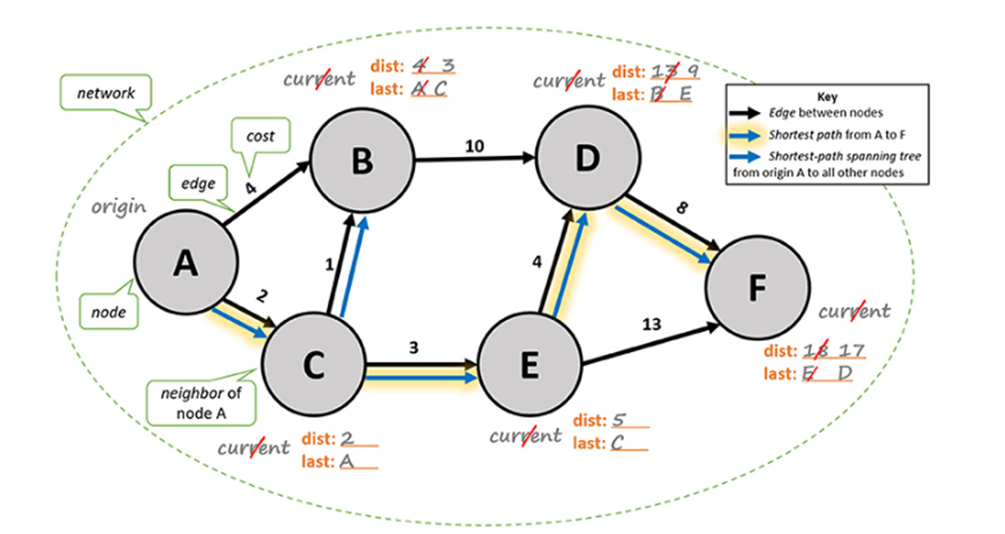
Figure
2: The shortest route from node A to node F in this network may be found by
following the blue arrows that have been highlighted
If
we wish to identify the shortest route between nodes A and F in the network
shown in Figure 2, we should pick the edges with the lowest costs. For
instance, we may pick the edge with a cost of 2 from node A to node C rather
than the one with a cost of 4 from node A to node B. One of the main concepts
of shortest path is selecting the edges with the lowest costs to determine the
shortest path.
English
Bengali
Chinese (Simplified)
French
German
Hindi
Japanese
Kannada
Latin
Marathi
Nepali
Spanish
Tamil
Telugu
Kalinga Plus is an initiative by Kalinga University, Raipur. The main objective of this to disseminate knowledge and guide students & working professionals.
This platform will guide pre – post university level students.
Pre University Level – IX –XII grade students when they decide streams and choose their career
Post University level – when A student joins corporate & needs to handle the workplace challenges effectively.
We are hopeful that you will find lot of knowledgeable & interesting information here.
Happy surfing!!